словосочетания.рф -
купить или арендовать доменное имя онлайн- Домены совпадающие с словосочетания
- Покупка
- Аренда
- словосочетания.рф
- 70 000
- 700
- Домены с переводом, содержащими словосочетани
- Покупка
- Аренда
- slovosochetanie.ru
- 50 000
- 500
- Доменное имя Эдисо
- Узнайте, почему приобретение или аренда доменного имени эдисон.рф является одним из перспективных и выгодных инвестиционных решений для вашего бизнеса в России.
- Шоферюга.рф: Эксклюзивное Доменное Имя - Путь К Успеху Вашего Бизнеса В Сети
- Овладейте лидерством своих текущих и потенциальных клиентов при помощи эксклюзивных доменного имени Шоферюга.рф, гарантирующим их доверие и выгодные показатели в сети.
- Доменное имя чуткость.рф: Путь к успеху для бизнеса и личного бренда
- Достигайте лучшей видимости в Интернете и укрепляйте свой бизнес или личный бренд с помощью стратегической покупки или аренды чуткость.рф - привлекательного и легко запоминающегося доменного имени, идеально подходящего для компаний и предпринимателей, кот
- Доменное имя чела.рф: выгода от покупки или аренды, советы для эффективного продвижения сайта
- Узнайте, какой вариант лучше для вашего сайта - приобрести доменное имя чела.рф или арендовать его, а также изучите советы по повышению эффективности вашего веб-ресурса.
- Заказать доменное имя целофанчик.рф: Решаем вашу уникальность и преимущества аренды в интернете
- Заказывай доменное имя целофанчик.рф - ключ к пиару, уникальности и лучшему SEO эффекту для вашего онлайн-представительства на нашем специализированном сайте, где доступны варианты покупки и аренды.
- Приобретение или аренда домена для церемоний: почему .рф - отличный выбор
- Узнайте, почему приобретение или аренда доменного имени 'церемония.рф' для вашего мероприятия является стратегическим ходом, гарантирующим легкий доступ и позиционирование в поисковых системах, а также солидное доверие аудитории к вашей деятельности.
- Регистрация домена кошечка.рф для вашего онлайн-проекта: незаменимый шаг к успеху
- Добавьте запоминающийся характер вашему интернет-проекту с доменом хэл.рф, идеально подходящим для личных и деловых целей, обеспечивая быстрый и легкий доступ к вашей онлайн-странице.
- Доменное имя хоть.рф: Лучший выбор для вашего онлайн-присутствия
- Погрузитесь в мир цифровой экономики с доменом хоф.рф и раскройте своё уникальное предложение, экономя время и деньги за счёт интуитивно понятного имени, оптимального для быстрого привлечения аудитории и повышения доверия к вашему бренду.
- Универсальное доменное имя уцененное.рф: выгодная аренда и покупка для успеха в интернете
- Оптимальный выбор для экономии средств и расширения онлайн-присутствия – приобрести или арендовать уцененное.рф: доступное решение для бизнеса и частных пользователей в цифровом пространстве России.
- Почему выгодно приобрести или арендовать доменное имя утепление.рф - ключ к успеху в сфере утепления
- Доменное имя хабы.рф: расширение для вашего онлайн-успеха - купить или арендовать без задержек
- Откройте двери к онлайн-успеху с доменным именем хабы.рф — идеальное решение для вашего проекта, предлагающее удобство покупки или аренды уже сегодня.
- Франчайзинг и мастерство выбора успешного доменного имени для проникновения на рынок
- Узнайте, как выбор подходящего доменного имени в контексте франчайзинга может стать ключом к успешному проникновению и удержанию позиций на конкурентном рынке.
- Аренда и покупка домена фейсбук.рф: стратегические преимущества для вашего бизнеса
- Аренда или покупка домена фейсбук.рф – стратегический ход для бизнеса, гарантирующий повышение узнаваемости и доверия клиентов в цифровой среде.
- Установки.рф: Как выбрать идеальное доменное имя для успеха бизнеса – критерии и стратегии
- Оптимизируйте онлайн-присутствие с установки.рф, выбирая идеальное доменное имя для вашего бизнеса: возможность купить или арендовать – стратегический ход к успеху в интернете.
- Хитрый выбор доменного имени для бизнеса: Почему хитовый.рф - идеальный вариант в интернете
- Откройте новые горизонты для вашего бизнеса с доменным именем хитовый.рф, сочетающим в себе запоминающуюся аутентичность и возможности российского сегмента Интернета, гарантируя повышение узнаваемости и привлечение целевой аудитории.
- Финансовое.рф - Ключ к успеху: Аренда или покупка доменного имени для быстрого развития бизнеса
- Узнайте, почему выбор между покупкой или арендой доменного имени на финансовом портале Финансовое.рф - ключевой шаг на пути к успеху в Интернете и укреплению вашего онлайн-престижа.
- Фасольки.рф: Как выбрать оптимальное доменное имя для бизнеса — покупка или аренда?
- Откройте новые горизонты для бизнеса с доменом Фасольки.рф – выбор между покупкой или арендой обеспечит эффективную онлайн-присутствие и конверсии!
- Домен тупицы.рф: Ваш ключ к успеху в онлайн-сфере - покупка или аренда
- Узнайте, какие неоспоримые преимущества и возможности открываются перед вами при покупке или аренде оригинального доменного имени 'тупица.рф', идеально подходящего для бизнеса, блоггинга или творческих целей.
- Купить или арендовать доменное имя в Тяни.РФ — Стратегии для успешного бизнеса
- Узнайте, почему покупка или аренда доменного имени Тяни.РФ может стать ключом к успеху вашего бизнеса, обеспечив запоминаемость, локальность и доверие вашего веб-сайта в регионе РФ.
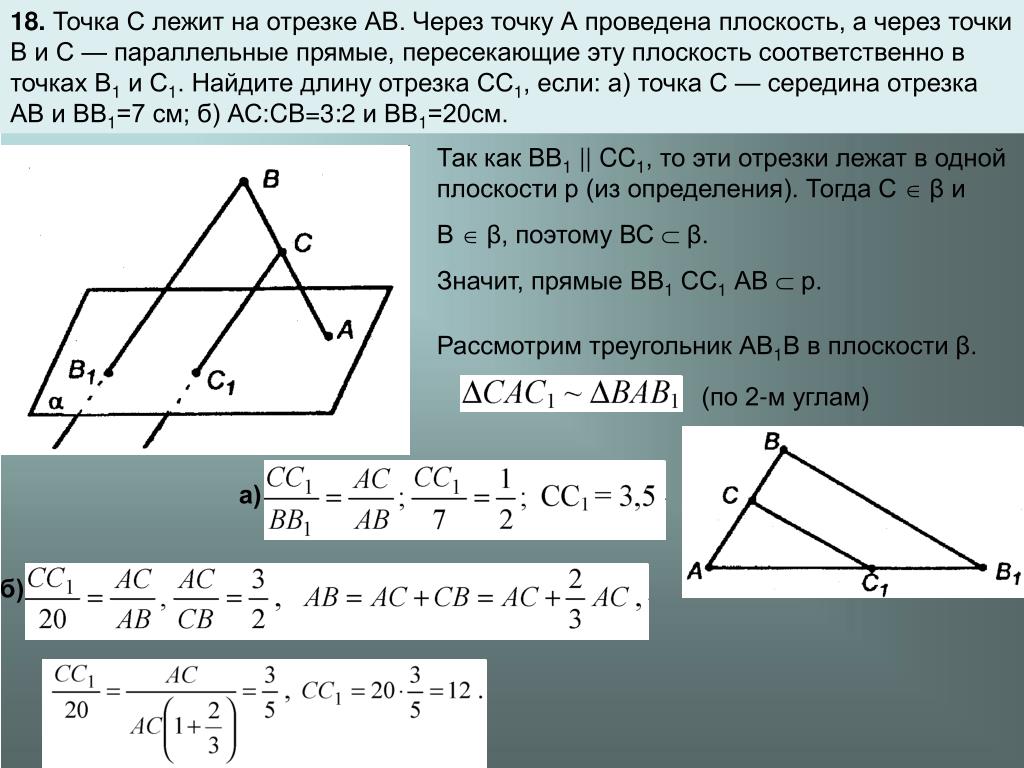
Точка расположена на отрезке, плоскость проходит через нее и параллельна двум данным прямым
Для начала, рассмотрим что такое точка с на отрезке ав. Это означает, что данная точка с лежит на отрезке, соединяющем две заданные точки а и в. Точка с находится между точками а и в и делит отрезок ав на две части в определенном отношении. Чтобы определить положение точки с на отрезке ав, мы можем использовать формулу нахождения координат точки по формуле с = (а + в)/2. Здесь а и в - координаты заданных точек, а с - координаты искомой точки с. Когда мы рассмотрим построение параллельных прямых в плоскости а через точки а и с, мы должны помнить о следующем. Для конструирования параллельной прямой, достаточно найти ее уравнение и использовать его для построения данной прямой. В данном случае мы знаем координаты точек а и с, и можем использовать эти данные для нахождения уравнения параллельной прямой. Что такое точка с на отрезке ав?Точка С на отрезке АВ играет важную роль в геометрии и математике в целом. Она позволяет решать различные задачи, связанные с расположением точек и отрезков в пространстве. Кроме того, точка С на отрезке АВ может использоваться для построения параллельных прямых в плоскости А, проходящих через точки А и С. Это свойство точки С помогает решать задачи по определению и построению параллельных линий и поверхностей.
Основные понятия и определенияПеред тем, как перейти к изучению точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с, полезно разобраться в некоторых основных понятиях.
Знание этих основных понятий и определений поможет нам лучше понять тему точки с на отрезке ав и параллельных прямых в плоскости а через точки а и с и успешно продолжить изучение данной темы. Как найти точку с на отрезке ав?Чтобы найти точку С на отрезке АВ, нам понадобятся координаты точек А и В. Представим отрезок АВ в виде прямой, проходящей через эти две точки. Для нахождения точки С, которая будет лежать на этой прямой и параллельна другой прямой в плоскости А, используем формулу: С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) Здесь t – параметр, принадлежащий отрезку [0, 1]. Если t = 0, то точка С будет совпадать с точкой А, если t = 1 – с точкой В. Итак, мы знаем координаты точек А и В, а также значения параметра t. Подставляем все это в формулу и получаем координаты точки С. Пример:
Пусть А(2, 3) и В(6, 9). Находим значений параметра t, например, t = 0.5. С(xС, yС) = A(xA, yA) + t * (B(xB, yB) - A(xA, yA)) С(xС, yС) = (2, 3) + 0.5 * ((6, 9) - (2, 3)) С(xС, yС) = (2, 3) + 0.5 * (4, 6) С(xС, yС) = (2, 3) + (2, 3) С(xС, yС) = (4, 6) Таким образом, точка С находится на середине отрезка АВ и имеет координаты (4, 6). Существование и уникальность точки CДля того чтобы точка C существовала на отрезке AB и была параллельна прямым в плоскости, проходящим через точки A и B, необходимо выполнение определенных условий. Во-первых, для существования точки C на отрезке AB необходимо, чтобы точка A не совпадала с точкой B, иначе отрезок будет вырожденным. Во-вторых, чтобы точка C была параллельна прямым, нужно убедиться, что отрезок AB и прямые в плоскости, проходящие через точки A и B, действительно параллельны. Это означает, что угол между отрезком AB и любой из этих прямых должен быть равен 180 градусам. Если все условия выполнены, то точка C существует и является уникальной на отрезке AB, параллельна прямым в плоскости, проходящим через точки A и B. Параллельные прямые в плоскости а
Если две прямые параллельны, то их наклоны равны. Наклон прямой определяется через разность координат точек, через которые проходит прямая. Например, если прямая проходит через точки (х1, у1) и (х2, у2), то наклон прямой равен: м = (у2 - у1) / (х2 - х1). Если наклоны двух прямых равны, то они параллельны. И наоборот, если две прямые параллельны, то их наклоны равны. Кроме определения параллельности через наклоны прямых, можно использовать еще один способ - построение плоскости а. Для этого необходимо провести прямую через две точки a и с, а затем, провести скрещивающую прямую через точку a, параллельную прямой о. Если эти две прямые не пересекаются, то прямая о и параллельна прямой в плоскости а.
Уравнения прямых о и а имеют одинаковую функцию (2х), поэтому их наклоны равны и они параллельны. Как найти параллельные прямые через точки а и с?Для того чтобы найти параллельные прямые, проходящие через заданные точки A и C на плоскости, необходимо выполнить следующие шаги: Шаг 1: Определите координаты точек A и C. Для этого вам понадобятся значения x и y для каждой из точек. Шаг 2: Определите уравнение прямой, проходящей через точку A. Для этого можно использовать формулу наклона прямой, которая выглядит следующим образом: y - y1 = m(x - x1), где m - наклон прямой, а (x1, y1) - координаты точки A. Шаг 3: Используя полученное уравнение, подставьте координаты точки C и решите полученное уравнение относительно переменной m. Таким образом, вы сможете определить наклон параллельной прямой. Шаг 4: Найдите уравнение параллельной прямой, проходящей через точку C, используя найденный наклон m и координаты точки C. Вы можете использовать формулу y - y1 = m(x - x1), где (x1, y1) - координаты точки C. Шаг 5: Проверьте полученное уравнение, подставив в него координаты точек A и C. Если оба значения равны, значит, прямая, построенная по уравнению, параллельна прямой, проходящей через заданные точки A и C. Таким образом, следуя этим шагам, вы сможете найти параллельные прямые, проходящие через заданные точки A и C на плоскости. Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ. Точка с на отрезке ав и параллельные прямые в плоскости а через точки а и с Статья рассказывает о плоскости, проходящей через точку А и параллельной прямым АВ и АС, лежащими на отрезке АВ.
|

 Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.
Понимание понятия точка с на отрезке ав и параллельные прямые является важным элементом в изучении геометрии и математики в целом. В данной статье мы рассмотрим основные принципы и правила для определения точки с на отрезке ав и построения параллельных прямых в плоскости а через заданные точки а и с.